block
 blinker
blinker  tub
tub  beehive
beehive  loaf
loaf  glider
glider 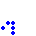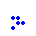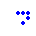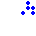 boat
boat  long boat
long boat  ship
ship  pond
pond  canoe
canoe 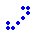 pulsar
pulsar 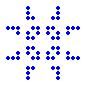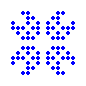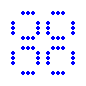
Below you can play a modified version of the game. Instead of being infinite, this board is 30 by 30 and the topology is like a donut; the top row is adjacent to the bottom and the left column is adjacent to the right. You can initialize the world randomly or in a line or in a square and you can toggle the state of a cell by clicking on it.
In July of 2007 I looked into creating animated GIFs and here's the result.
Here are some common Game of Life constellations:
block  blinker
blinker  tub
tub  beehive
beehive  loaf
loaf  glider
glider 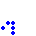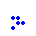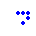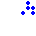 boat
boat  long boat
long boat  ship
ship  pond
pond  canoe
canoe 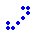 pulsar
pulsar 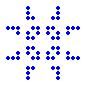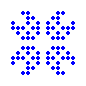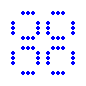
For each of the following links I started with a cross where the four line segements have the same lengths. The following numbers indicate these lengths.
11 This is the simplest start of this form which leads to a final population greater than twelve.
15 This is the simplest start of this form which generates gliders that continue forever.
33 This scenario takes much longer to stabalize than all starting configurations with shorter lengths.
34 This scenario stablizes with a greater variety of constellations.
78 This is the simplest start of this form that stabalizes with pulsars. It also has several colliding gliders. (warning: this gif has a 2.6 megabyte size)